문제
철수의 토마토 농장에서는 토마토를 보관하는 큰 창고를 가지고 있다. 토마토는 아래의 그림과 같이 격자모양 상자의 칸에 하나씩 넣은 다음, 상자들을 수직으로 쌓아 올려서 창고에 보관한다.
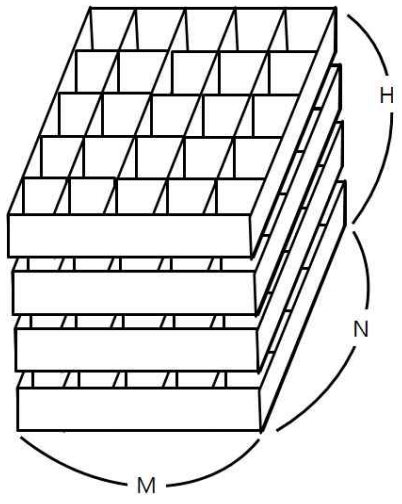
창고에 보관되는 토마토들 중에는 잘 익은 것도 있지만, 아직 익지 않은 토마토들도 있을 수 있다. 보관 후 하루가 지나면, 익은 토마토들의 인접한 곳에 있는 익지 않은 토마토들은 익은 토마토의 영향을 받아 익게 된다. 하나의 토마토에 인접한 곳은 위, 아래, 왼쪽, 오른쪽, 앞, 뒤 여섯 방향에 있는 토마토를 의미한다. 대각선 방향에 있는 토마토들에게는 영향을 주지 못하며, 토마토가 혼자 저절로 익는 경우는 없다고 가정한다. 철수는 창고에 보관된 토마토들이 며칠이 지나면 다 익게 되는지 그 최소 일수를 알고 싶어 한다.
토마토를 창고에 보관하는 격자모양의 상자들의 크기와 익은 토마토들과 익지 않은 토마토들의 정보가 주어졌을 때, 며칠이 지나면 토마토들이 모두 익는지, 그 최소 일수를 구하는 프로그램을 작성하라. 단, 상자의 일부 칸에는 토마토가 들어있지 않을 수도 있다.
입력
첫 줄에는 상자의 크기를 나타내는 두 정수 M,N과 쌓아올려지는 상자의 수를 나타내는 H가 주어진다. M은 상자의 가로 칸의 수, N은 상자의 세로 칸의 수를 나타낸다. 단, 2 ≤ M ≤ 100, 2 ≤ N ≤ 100, 1 ≤ H ≤ 100 이다. 둘째 줄부터는 가장 밑의 상자부터 가장 위의 상자까지에 저장된 토마토들의 정보가 주어진다. 즉, 둘째 줄부터 N개의 줄에는 하나의 상자에 담긴 토마토의 정보가 주어진다. 각 줄에는 상자 가로줄에 들어있는 토마토들의 상태가 M개의 정수로 주어진다. 정수 1은 익은 토마토, 정수 0 은 익지 않은 토마토, 정수 -1은 토마토가 들어있지 않은 칸을 나타낸다. 이러한 N개의 줄이 H번 반복하여 주어진다.
토마토가 하나 이상 있는 경우만 입력으로 주어진다.
출력
여러분은 토마토가 모두 익을 때까지 최소 며칠이 걸리는지를 계산해서 출력해야 한다. 만약, 저장될 때부터 모든 토마토가 익어있는 상태이면 0을 출력해야 하고, 토마토가 모두 익지는 못하는 상황이면 -1을 출력해야 한다.
풀이
백준 7576번 토마토의 3차원 버전이다. 기본적인 풀이는 백준 2178번 미로탐색과 비슷한 면이 있다. 다만, 미로탐색과는 다르게 맨 마지막 index에서 최댓값을 갖는다는 보장이 없으므로, 최댓값을 기록하면서 갈 필요가 있다.
배운 점
1) 3차원 matrix의 저장
numpy를 쓴다면 편하게 할 수 있겠으나, 코딩테스트를 준비하는 현 상황에서 외부 라이브러리를 '지금' 익힐 필요는 없어보인다. input값을 편하게 저장하려면, [z][x][y]순으로 정렬받는 것이 좋다.
2) exit(): input값으로 0을 넣으면 프로그램이 성공적으로 종료됐음을 나타내며, 0 외의 수를 넣으면 오류를 나타냄.
여태까지 for문 여러개면 break 여러 번 쓰고 break 됐는지 확인하는 boolean 변수 선언했는데, 그럴 필요가 없다.
참고: https://stackoverflow.com/questions/9426045/difference-between-exit0-and-exit1-in-python/9426115
코드
# 7576 3차원 버전
import sys, collections
dx = [-1, 1, 0, 0, 0, 0]
dy = [0, 0, -1, 1, 0, 0]
dz = [0, 0, 0, 0, -1, 1]
N, M, H = map(int, sys.stdin.readline().split())
farm = [[] for _ in range(H)]
for k in range(H):
for i in range(M):
farm[k].append(list(map(int, sys.stdin.readline().split())))
queue= collections.deque()
max_num = 1
for k in range(H):
for i in range(M):
for j in range(N):
if farm[k][i][j] == 1:
queue.append((k, i, j))
while queue:
z, x, y = queue.popleft()
for i in range(6):
nx = x + dx[i]
ny = y + dy[i]
nz = z + dz[i]
if 0 <= nx < M and 0 <= ny < N and 0 <= nz < H:
if farm[nz][nx][ny] == 0:
farm[nz][nx][ny] = farm[z][x][y] + 1
max_num = farm[nz][nx][ny]
queue.append((nz, nx, ny))
for k in range(H):
for i in range(M):
if 0 in farm[k][i]:
print(-1)
exit(0)
print(max_num - 1)'PS > BFS & DFS' 카테고리의 다른 글
| 백준 13549번: 숨바꼭질3 (JAVA) TODO (0) | 2022.02.15 |
|---|---|
| 백준 20304번: 비밀번호 제작 (JAVA) (0) | 2022.02.14 |
| 백준 1697번: 숨바꼭질 (Python) (0) | 2021.11.29 |
| 백준 2178번: 미로 탐색 (Python) (0) | 2021.11.29 |
| Leetcode 207: Course Schedule (Python) (0) | 2021.11.28 |